Progressão Aritmética (P.A): Definição, propiedades, exemplos
Uma Progressão Aritmética é uma sequência na qual a diferença entre quaisquer dois termos consecutivos é sempre constante. Essa constante é chamada de razão da progressão aritmética, sendo representada pela letra r.
Com aplicações em diversas áreas da matemática e ciências, as Progressões Aritméticas tiveram contribuições de diversos matemáticos ao longo da história, como Carl Friedrich Gauss, que aos 10 anos descobriu a fórmula para a soma dos termos de uma Progressão Aritmética finita.
Conta a história que Gauss, desafiado por seu professor a somar os números de 1 a 100, percebeu que poderia agrupar os números em pares que somavam 101, obtendo assim a soma de 5050.
Termo Geral da Progressão Aritmética
Formalmente, uma Progressão Aritmética é definida pela fórmula do termo geral:

Onde:
- - an é o n-ésimo termo da sequência.
- - a1 é o primeiro termo da sequência.
- - n é o número do termo desejado.
- - r é a razão da progressão.
Exemplos de Progressão Aritmética
Exemplo 1:
Vamos considerar uma Progressão Aritmética simples com a1 = 2 e r = 3. Neste caso, os primeiros cinco termos seriam:
- a1 = 2
- a2 = 2 + (2-1) . 3 = 5
- a3 = 2 + (3-1) . 3 = 8
- a4 = 2 + (4-1) . 3 = 11
- a5 = 2 + (5-1) . 3 = 14
Portanto, a sequência gerada seria: 2, 5, 8, 11, 14.
Exemplo 2:
Agora, consideremos uma Progressão Aritmética com a1 = 10 e r = -2. Os primeiros cinco termos seriam:
- a1 = 10
- a2 = 10 + (2-1) . (-2) = 8
- a3 = 10 + (3-1) . (-2) = 6
- a4 = 10 + (4-1) . (-2) = 4
- a5 = 10 + (5-1) . (-2) = 2
Portanto, a sequência gerada seria: 10, 8, 6, 4, 2.
Classificação de uma PA
As Progressões Aritméticas podem ser classificadas com base no valor da razão, sendo categorizadas da seguinte maneira:
- 1. Constante: Nesse caso, a razão é igual a zero, como na sequência (2, 2, 2, 2, 2...), onde r = 0.
- 2. Crescente: Quando a razão é maior que zero, a progressão aritmética é considerada crescente, como na sequência (1, 2, 3, 4, 5...), onde r = 1.
- 3. Decrescente: Se a razão for menor que zero, a progressão é classificada como decrescente, como na sequência (5, 4, 3, 2, 1, 0, -1...), com r = -1.
Propiedades da PA
1ª Propiedade: A soma de dois termos equidistantes de uma PA finita, sempre será igual a soma de seus extremos.
Exemplo: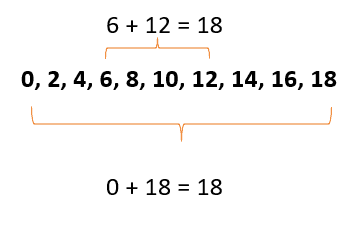
2ª Propiedade: Ao considerar três termos consecutivos de uma Progressão Aritmética, o termo do meio é igual à média aritmética dos outros dois termos.
Exemplo:
3ª Propiedade: Em uma Progressão Aritmética finita com um número ímpar de termos, o termo central será igual à média aritmética entre termos que estão igualmente distantes dele. Essa característica é uma derivação da 1ª propiedade.
Exemplo:
Soma dos termos de Uma P.A finita
Para calcular a soma dos termos de uma Progressão Aritmética finita, basta aplicar a seguinte fórmula:

Onde:
- - Sn representa a soma dos termos da PA .
- - a1 é o primeiro termo da PA.
- - an é a enésima posição da PA.
- - n é posição do termo.
Vamos tomar como exemplo a nossa última PA: 0, 2, 4, 6, 8, 10, 12, 14, 16 com nove termos:

